Содержание
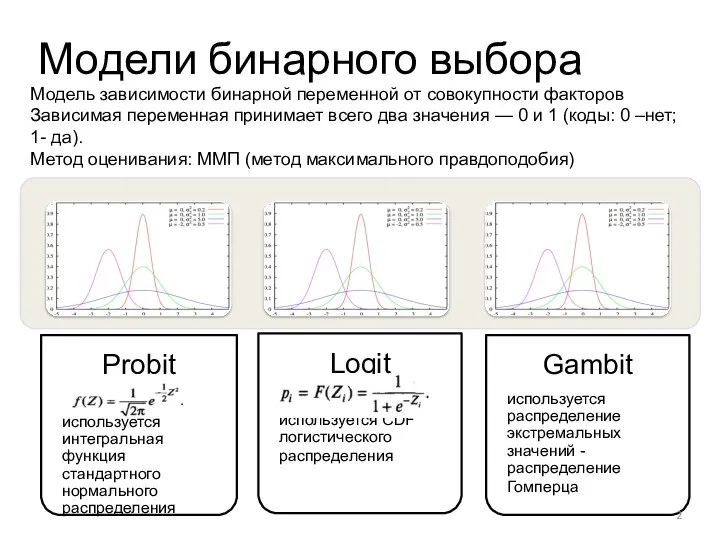
- 2. НИУ ВШЭ , Москва, 2013 Модели бинарного выбора photo photo photo Модель зависимости бинарной переменной от
- 3. НИУ ВШЭ , Москва, 2013 Алгоритм построения модели photo photo photo Определение зависимой переменной и факторов
- 4. НИУ ВШЭ , Москва, 2013 Алгоритм построения модели photo photo photo Медицина (определение вероятности успешного лечения
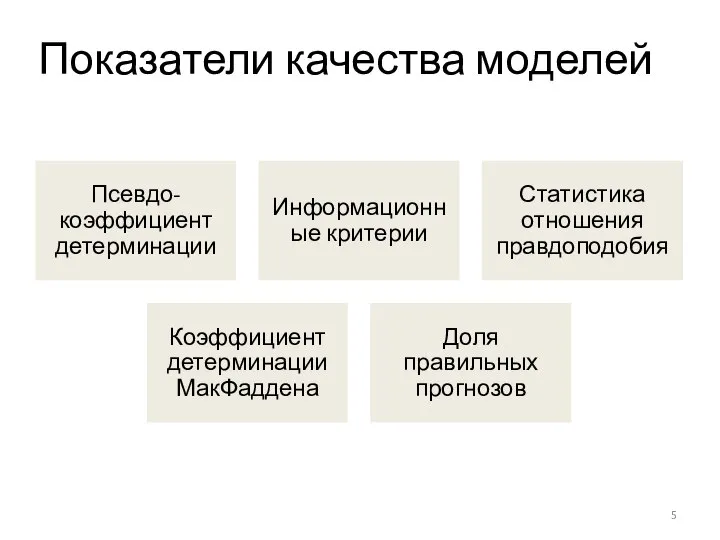
- 5. НИУ ВШЭ , Москва, 2013 photo photo photo Показатели качества моделей Показатели качества моделей
- 6. НИУ ВШЭ , Москва, 2013 photo photo photo Показатели качества моделей Показатели качества моделей: Информационные критерии
- 7. НИУ ВШЭ , Москва, 2013 photo photo photo Преимущества и недостатки моделей: Преимущества Недостатки Исправление недостатка
- 8. Пример 1: соц. исследование Исследование факторов, влияющих на вероятность окончания средней школы Зависимая переменная: GRAD окончание
- 9. (Подставляется полученное выражение для Z) 3) 4) Таблица оцененных коэффициентов. Далее для оценки кумулятивного и предельного
- 10. Пример нахождения выражения предельного эффекта для одной из переменных Столбец предельных эффектов Пример 1: верификация модели
- 11. Интерпретация коэффициентов: отношения шансов Увеличение ASVABC на один балл увеличивает вероятность успешного окончания школы на 0,4
- 12. Пример 2: финансовый менеджмент Зависимая переменная: вероятность участия российских компаний в межфирменных отношениях Предикторы: факторы окружающей
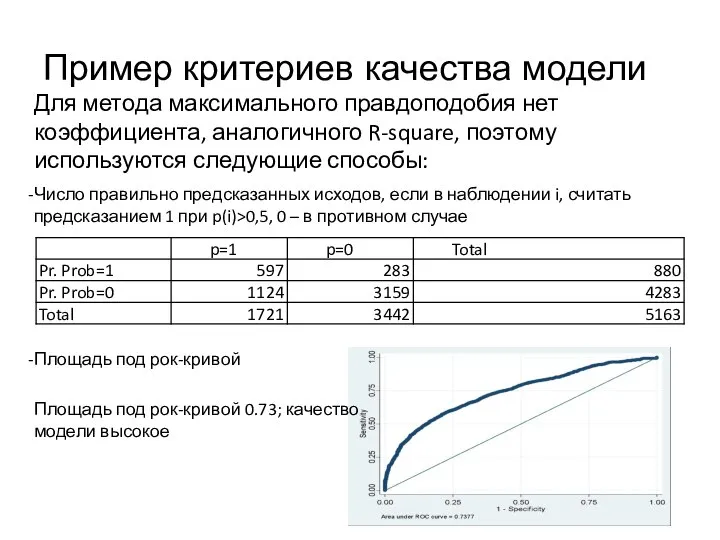
- 13. Пример критериев качества модели Для метода максимального правдоподобия нет коэффициента, аналогичного R-square, поэтому используются следующие способы:
- 14. Пример 3: A model for Happiness Измерение уровня удовлетворенности населения жизнью Зависимая переменная: уровень удовлетворенности (индекс
- 16. НИУ ВШЭ , Москва, 2013 photo photo photo Области применения моделей: маркетинг Изучение поведения покупателей Зависимая
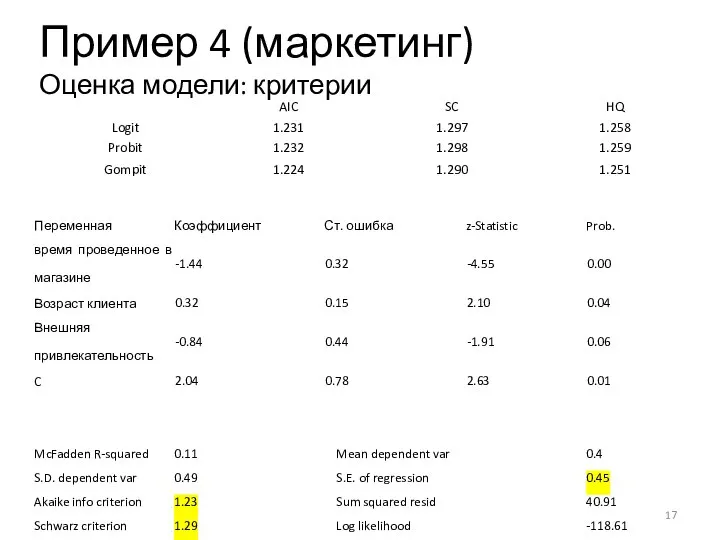
- 17. НИУ ВШЭ , Москва, 2013 photo photo photo Пример №1 Пример 4 (маркетинг) Оценка модели: критерии
- 18. НИУ ВШЭ , Москва, 2013 photo photo photo Stefan Boes, Rainer Winkelmann (2004) «Income and Happiness»
- 20. Скачать презентацию













 Центры ответственности. Виды центров ответственности. Политика работы с центрами ответственности
Центры ответственности. Виды центров ответственности. Политика работы с центрами ответственности Методы оценки риска
Методы оценки риска Концепция и функции логистики. Тема 2
Концепция и функции логистики. Тема 2 Совместные закупки СИМА ЛЕНД
Совместные закупки СИМА ЛЕНД История развития теории управления проектами
История развития теории управления проектами Менеджменттегі бақылау
Менеджменттегі бақылау Структура бизнеса ГК Менеджмент
Структура бизнеса ГК Менеджмент Обучение и развитие персонала. Деловая карьера
Обучение и развитие персонала. Деловая карьера Менеджмент. Виды стратегий
Менеджмент. Виды стратегий Требования к системе в виде модели. Область применения и ограничения
Требования к системе в виде модели. Область применения и ограничения Оценка персонала
Оценка персонала Кадровая политика
Кадровая политика Модуль синхронизации Slack space пользователей с LDAP
Модуль синхронизации Slack space пользователей с LDAP Педагогічний менеджмент як галузь знань та сфера діяльності
Педагогічний менеджмент як галузь знань та сфера діяльності Основы стратегического менеджмента
Основы стратегического менеджмента Технологии мониторинга, гуманитарной экспертизы и социального аудита образовательных систем
Технологии мониторинга, гуманитарной экспертизы и социального аудита образовательных систем Принципы построения систем управления
Принципы построения систем управления Конкурентноспособность туристического предприятия
Конкурентноспособность туристического предприятия Технико-экономические особенности отдельных видов транспорта
Технико-экономические особенности отдельных видов транспорта Оценка и профессиональное развитие персонала
Оценка и профессиональное развитие персонала Коммуникации в менеджменте. Технологии самоорганизации и эффективность взаимодействия
Коммуникации в менеджменте. Технологии самоорганизации и эффективность взаимодействия Как понравится рекламодателю на первой встрече?
Как понравится рекламодателю на первой встрече? Возвратные логистические потоки в электронной коммерции
Возвратные логистические потоки в электронной коммерции Оценка персонала организации
Оценка персонала организации Мотивации для менеджеров. Карьерная лестница
Мотивации для менеджеров. Карьерная лестница Управление организационными изменениями
Управление организационными изменениями Имидж успешного руководителя
Имидж успешного руководителя Деловые коммуникации
Деловые коммуникации