Содержание
- 2. 3. ВЫПУКЛЫЕ ФУНКЦИИ (ПРОДОЛЖЕНИЕ) 3.4. Дифференцируемость выпуклой функции по всем возможным направлениям. 3.3. Непрерывность выпуклой функции.
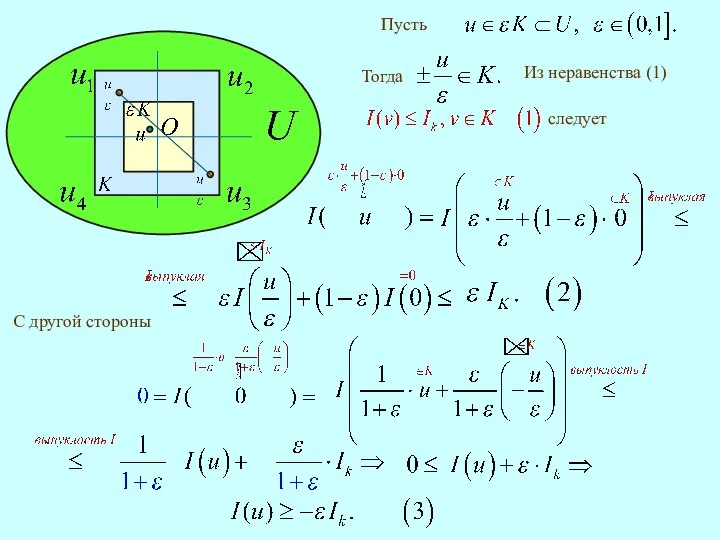
- 3. 3.3. Непрерывность выпуклой функции. оказывается столь сильным, Теорема 6. выпукла. Доказательство. Сначала предположим, что с центром
- 4. Из неравенства (1) следует С другой стороны
- 5. Общий случай сводится к уже рассмотренному определенной формулой Тогда по доказанному она непрерывна в нуле. Непрерывной
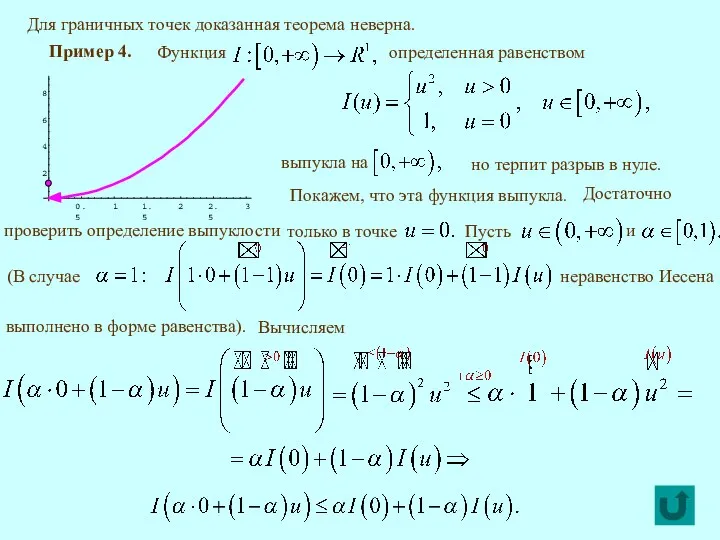
- 6. Для граничных точек доказанная теорема неверна. Пример 4. но терпит разрыв в нуле. Покажем, что эта
- 7. 3.4. Дифференцируемость выпуклой функции по всем возможным направлениям. Определение 3. такое, что Пример 5. Пример 6.
- 8. Пример 7. имеется хотя бы одно возможное направление. и содержит не менее двух точек. Определение 4.
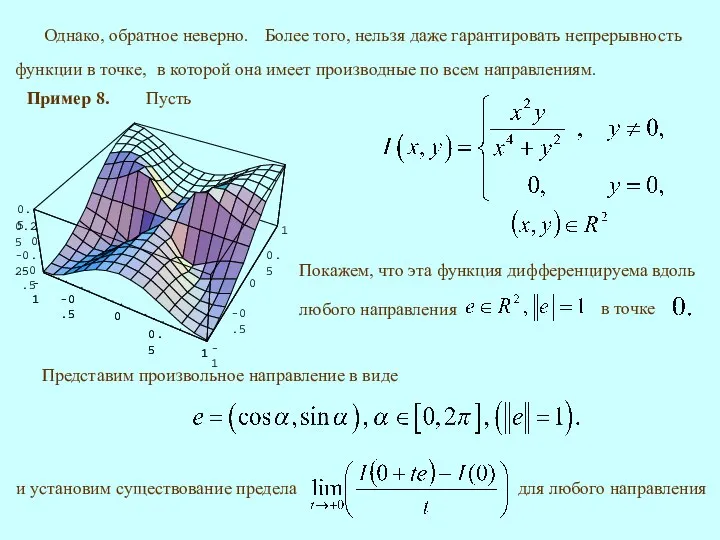
- 9. в которой она имеет производные по всем направлениям. Пример 8. Пусть Однако, обратное неверно. Представим произвольное
- 10. Отсюда выводим Таким образом, указанный предел существует.
- 11. Тогда Теорема 7. выпукла. Доказательство. Имеет место включение С другой стороны
- 12. Тогда
- 13. Имеет место равенство Тогда
- 15. Упражнение 1. Решение. Функция нормы выпукла и конечна.
- 17. Скачать презентацию







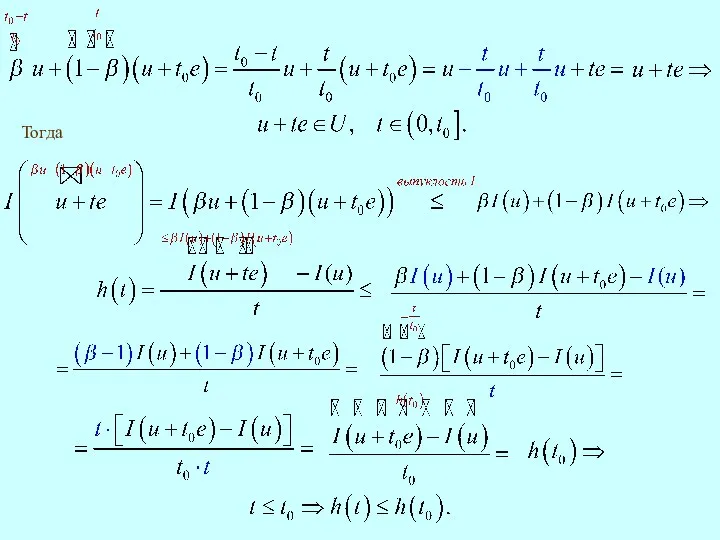



 Эффект модификации и взаимодействия
Эффект модификации и взаимодействия Аттестационная работа. Современные педагогические технологии в сфере физической культуры и спорта
Аттестационная работа. Современные педагогические технологии в сфере физической культуры и спорта Гражданское право как отрасль права
Гражданское право как отрасль права Геополитика и международные отношения
Геополитика и международные отношения Алгоритмы удаления невидимых линий и поверхностей
Алгоритмы удаления невидимых линий и поверхностей Структура и содержание контрольных измерительных материалов (КИМ) единого государственного экзамена (ЕГЭ)
Структура и содержание контрольных измерительных материалов (КИМ) единого государственного экзамена (ЕГЭ) Плоские железобетонные перекрытия
Плоские железобетонные перекрытия Византийские мозаики Работу выполнила Ученица 10 класса МБУ ОО СОШ №15 Васильева Валерия
Византийские мозаики Работу выполнила Ученица 10 класса МБУ ОО СОШ №15 Васильева Валерия  Метод анализа иерархий
Метод анализа иерархий Лекция защита информации
Лекция защита информации  Анализ мероприятий по обеспечению экологической безопасности
Анализ мероприятий по обеспечению экологической безопасности Теория жизненного цикла П.Херси и К.Бланшара Выполнила: студентка 3-го курса ФТД группы Т-083 Восколович Юля
Теория жизненного цикла П.Херси и К.Бланшара Выполнила: студентка 3-го курса ФТД группы Т-083 Восколович Юля  Животный мир - презентация для начальной школы
Животный мир - презентация для начальной школы Презентация на тему "Памир - 2014" - скачать презентации по Педагогике
Презентация на тему "Памир - 2014" - скачать презентации по Педагогике Процесс художественной коммуникации и его роль в сближении народов, стран, эпох. «Искусство» 8 класс
Процесс художественной коммуникации и его роль в сближении народов, стран, эпох. «Искусство» 8 класс Наследование
Наследование  Средства тиражирования документов. Классификация
Средства тиражирования документов. Классификация Религии Японии. Синтоизм
Религии Японии. Синтоизм Алгоритмізація та програмування. Поняття алгоритму. Властивості алгоритму. Форми подання алгоритму
Алгоритмізація та програмування. Поняття алгоритму. Властивості алгоритму. Форми подання алгоритму Модуль Календарное планирование
Модуль Календарное планирование Социологическая трактовка личности
Социологическая трактовка личности ХРОНИЧЕСКИЕ ЗАБОЛЕВАНИЯ ПОЧЕК: КЛАССИФИКАЦИЯ, КЛИНИЧЕСКИЙ ПОДХОД И ЛЕЧЕНИЕ В ДОДИАЛИЗНОМ ПЕРИОДЕ
ХРОНИЧЕСКИЕ ЗАБОЛЕВАНИЯ ПОЧЕК: КЛАССИФИКАЦИЯ, КЛИНИЧЕСКИЙ ПОДХОД И ЛЕЧЕНИЕ В ДОДИАЛИЗНОМ ПЕРИОДЕ  Контрольно-кассовая техника
Контрольно-кассовая техника Определение типа суждения. Подготовка к ЕГЭ по обществознанию
Определение типа суждения. Подготовка к ЕГЭ по обществознанию GPS трекер
GPS трекер Презентация "елочные игрушки Гараевой" - скачать презентации по МХК
Презентация "елочные игрушки Гараевой" - скачать презентации по МХК Презентация на тему "МОДЕРНИЗАЦИЯ ОБРАЗОВАНИЯ" - скачать презентации по Педагогике
Презентация на тему "МОДЕРНИЗАЦИЯ ОБРАЗОВАНИЯ" - скачать презентации по Педагогике И.Крамской Портрет художника И. И. Шишкина
И.Крамской Портрет художника И. И. Шишкина