Содержание
- 2. Квадратное уравнение. ах² + bх + с = 0, х – переменная, а, b, с– числа,
- 3. Неполное квадратное уравнение. с = 0, ах ² + bх = 0, х (ах + b)
- 4. Неполное квадратное уравнение. b = 0, ах ²+ с = 0, х ² = – c/a;
- 5. Неполное квадратное уравнение. b = 0, c = 0, ах ²= 0, х ² = 0,
- 6. Квадратное уравнение ах² + bх + с = 0 D = b ² – 4ac; D
- 7. аx ² + 2kx + c = 0, D1 = k ² – ac; D1 >
- 8. Приведённое квадратное уравнение. x² + px + q = 0, по теореме Виета, если х1, х2
- 9. Приведённое квадратное уравнение. x² + px + q = 0, если p = 2k, то Р
- 10. Решение уравнения методом разложения его левой части на множители. ах² + bх + с = 0,
- 11. Решение квадратного уравнения , используя свойства коэффициентов. ах² + bх + с = 0, Если a
- 12. Решение квадратного уравнения , используя свойства коэффициентов. ах² + bх + с = 0, Если a
- 13. Графический способ решения квадратных уравнений. ах² + bх + с = 0, ах² = - bх
- 14. Биквадратное уравнение 4 ах + bх² + с = 0, а ≠ 0, х -переменная, а,
- 16. Скачать презентацию













 Ряды и интеграл Фурье
Ряды и интеграл Фурье Решение треугольников
Решение треугольников Алгоритмы старинных задач
Алгоритмы старинных задач Свойства параллельных прямых
Свойства параллельных прямых История Кремля в математике и литературе
История Кремля в математике и литературе Аттестационная работа. Математическое моделирование производственных процессов
Аттестационная работа. Математическое моделирование производственных процессов Умножение числа на ноль и единицу
Умножение числа на ноль и единицу Правила сравнения чисел
Правила сравнения чисел Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Решение задач на проценты
Решение задач на проценты Презентация на тему Математические ребусы
Презентация на тему Математические ребусы  Численное моделирование. Метод наименьших квадратов. (Лекция 7)
Численное моделирование. Метод наименьших квадратов. (Лекция 7) Аттестационная работа. 8 - 9 классы. Это удивительное понятие «функция»
Аттестационная работа. 8 - 9 классы. Это удивительное понятие «функция» Метрологическая аттестация средств измерений
Метрологическая аттестация средств измерений Презентация по математике "Совиниада" - скачать
Презентация по математике "Совиниада" - скачать  В царстве смекалки
В царстве смекалки Доли. Обыкновенные дроби
Доли. Обыкновенные дроби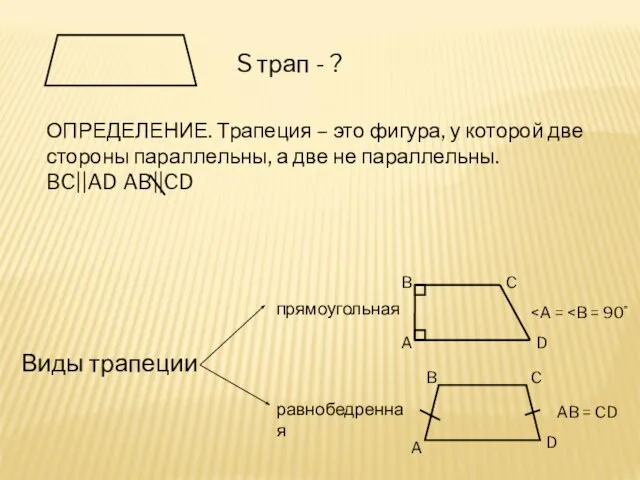 Площадь трапеции
Площадь трапеции Презентация на тему 2 класс Математический диктант №4
Презентация на тему 2 класс Математический диктант №4  Углы, вписанные в окружность
Углы, вписанные в окружность  Задания типа С5
Задания типа С5 Нахождение 2 чисел по их сумме и разности (в мире животных и птиц). Урок 2
Нахождение 2 чисел по их сумме и разности (в мире животных и птиц). Урок 2 Решение показательных уравнений
Решение показательных уравнений Случайная погрешность
Случайная погрешность решение неравенств с одной переменной
решение неравенств с одной переменной Площадь. Равновеликие и равносоставленные фигуры
Площадь. Равновеликие и равносоставленные фигуры Проект «Золотое сечение»
Проект «Золотое сечение» Функция. 7 класс
Функция. 7 класс