Содержание
- 2. Тема 1. Матрицы и определители §1. Понятие матрицы. Действия с матрицами Прямоугольной матрицей размера m×n называется
- 3. Любая матрица, имеющая одинаковое число строк и столбцов (m=n), называется квадратной матрицей порядка n. Её элементы
- 4. Важную роль в теории матриц играют следующие частные виды матриц: матрица-столбец (матрица размера m×1) матрица-строка (матрица
- 5. треугольная матрица – квадратная матрица, в которой все элементы выше (ниже) главной диагонали равны нулю диагональная
- 6. cкалярная матрица – диагональная матрица, все элементы которой равны (a11=a22=…=ann=λ) единичная матрица – скалярная матрица при
- 7. Действия с матрицами 1. Две матрицы A=(aij) и B=(bij) называются равными, если они одного размера и
- 8. 3. Операция умножения матрицы на число: tA=At=(t aij). Свойства операции: t⋅(l⋅A)=(t⋅l)⋅A; (t+l)⋅A=t⋅A+l⋅A; t⋅(A+B)=t⋅A+t⋅B.
- 9. Пример. Найти матрицу C=2A+4B, если
- 10. 4. Операция умножения матрицы Am×n на матрицу Bk×p определена только в том случае, если число столбцов
- 11. Тогда произведением матрицы A размера m×n со строками A1, A2,…, Am на матрицу B размером n×p
- 12. Пример 1. Вычислить произведение матриц
- 13. Пример 2. Вычислить значение многочлена f(x)=3x2 −2x+5 от матрицы
- 14. Свойства операции умножения матриц:
- 15. 5. Транспонированием матрицы называется операция замены строк матрицы её столбцами с сохранением их номеров. Например, если
- 16. Свойства операции транспонирования:
- 17. §2. Определители и их свойства Понятие определителя вводится только для квадратных матриц и при n≥3 связано
- 18. Пример. Найти алгебраические дополнения матрицы третьего порядка.
- 19. Тогда
- 20. Определитель n-го порядка вводится по индукции аналогичным образом через определители (n−1)-го порядка: Краткая запись:
- 21. Пример. Вычислить определитель матрицы
- 22. Свойства определителей: Определитель транспонированной матрицы равен определителю исходной матрицы: det AT=det A. При перестановке местами двух
- 23. Часто определители удобно вычислять, используя их свойства. Например, определитель удобно разлагать по строке (столбцу), содержащей нули,
- 24. §3. Обратная матрица Матрица B=A−1 называется обратной к квадратной матрице A, если A⋅A−1=A−1⋅A=E. Замечание. Не для
- 25. Если для матрицы A существует обратная A−1, то матрица называется обратимой (или невырожденной). В противном случае
- 26. Теорема. Если определитель матрицы A отличен от нуля, то обратная матрица A−1 существует и вычисляется по
- 27. Пример1. Найти обратную матрицу для
- 28. Пример2. Найти обратную матрицу для
- 29. Решение матричных уравнений С помощью обратной матрицы можно решить матричное уравнение АХ = В (или ХА
- 30. Пример 1. Решить матричное уравнение A X B = C, где
- 31. Пример 2. Решить матричное уравнение
- 32. Вычисление обратной матрицы методом элементарных преобразований Рассмотрим следующие элементарные преобразования матрицы: 1) перестановка строк (столбцов); 2)
- 33. Для отыскания обратной матрицы A−1 следует: 1) построить расширенную матрицу (A|E), приписывая к матрице A справа
- 34. Пример. Найти обратную матрицу A−1 для матрицы
- 35. Решение матричного уравнения методом элементарных преобразований Для решения уравнения вида АХ = В следует: 1) построить
- 36. Для решения уравнения вида ХА= В следует: 1) транспонировать исходное уравнение (ХА)Т= ВТ, тогда АТХТ= ВТ
- 38. Скачать презентацию



































 Интервальное оценивание
Интервальное оценивание Четырехугольники. Его компоненты и свойства
Четырехугольники. Его компоненты и свойства Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости Палички Непера
Палички Непера Геометрический метод решения задачи линейного программирования
Геометрический метод решения задачи линейного программирования Линейные неравенства с одним неизвестным
Линейные неравенства с одним неизвестным Методы решения уравнений
Методы решения уравнений Зарождение алгебры
Зарождение алгебры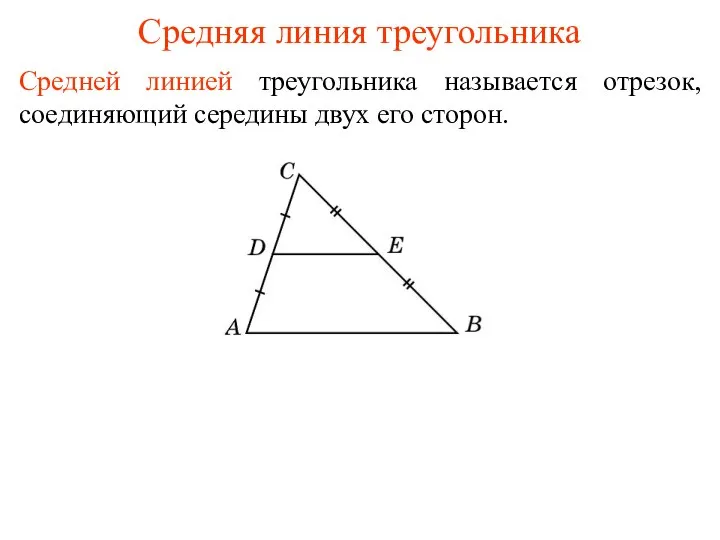 Средняя линия треугольника
Средняя линия треугольника Решение систем линейных алгебраических уравнений
Решение систем линейных алгебраических уравнений Математическое моделирование автоматических систем регулирования
Математическое моделирование автоматических систем регулирования Теория вероятностей. Случайные величины
Теория вероятностей. Случайные величины Рациональ саннар белән гамәлләр башкару
Рациональ саннар белән гамәлләр башкару Множество и его элементы
Множество и его элементы Центральные и вписанные углы
Центральные и вписанные углы Призма
Призма Преобразование графиков функции
Преобразование графиков функции Функцияны туынды арқылы зерттеу
Функцияны туынды арқылы зерттеу Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Признаки равенства треугольников
Признаки равенства треугольников Сравнение, сложение и вычитание дробей с разными знаменателями и смешанных чисел.
Сравнение, сложение и вычитание дробей с разными знаменателями и смешанных чисел.  Математика и искусство
Математика и искусство Деление с остатком
Деление с остатком 5 класс
5 класс  Интернет ресурсы при подготовке к ГИА по математике
Интернет ресурсы при подготовке к ГИА по математике Презентация по математике "Математика и русский язык: сотрудничество или конфликт?" - скачать бесплатно
Презентация по математике "Математика и русский язык: сотрудничество или конфликт?" - скачать бесплатно Вычитание
Вычитание Числовые последовательности. 9 класс
Числовые последовательности. 9 класс