Свойство касательной плоскости:
Т: радиус сферы, проведенный в точку касания, перпендикулярен к
касательной плоскости.
Доказательство:
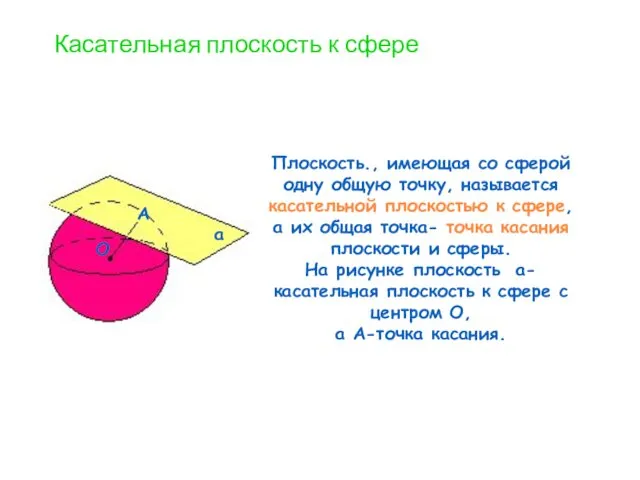
Рассмотрим рисунок, показанный ранее. Предположим, что радиус
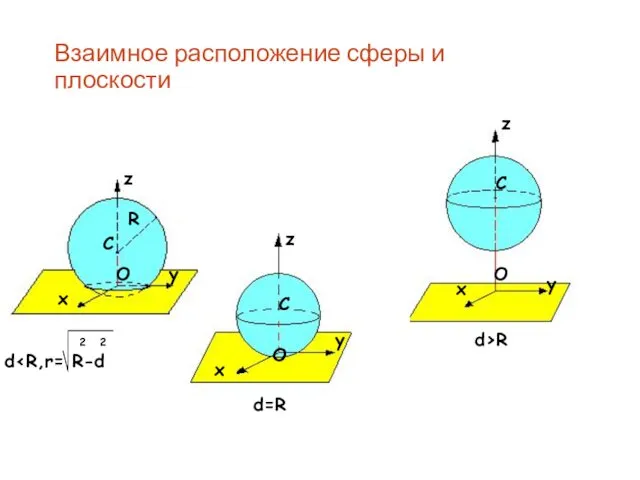
не перпендикулярен к плоскости. Тогда он является наклонной к плоскости а, то есть расстояние от сферы до плоскости меньше радиуса сферы, то есть они пересекаются по окружности, а это невозможно, так как а- касательная. Значит радиус перпендикулярен к плоскости, ч. т. д.
Обратная теорема: если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость- касательная к сфере
Доказательство:
Из условия следует, что радиус- перпендикуляр, проведённый из центра сферы к плоскости. Значит, расстояние от центра сферы до плоскости = радиусу, сфера и плоскость имеют одну общую точку, то есть данная плоскость- касательная к сфере, ч. т. д.





 Трофеи от Аничкова
Трофеи от Аничкова Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Сфера. Шар. Части сферы и шара
Сфера. Шар. Части сферы и шара Весь курс геометрии. (7 класс)
Весь курс геометрии. (7 класс) Аттестационная работа. Магические квадраты
Аттестационная работа. Магические квадраты Призмы и антипризмы
Призмы и антипризмы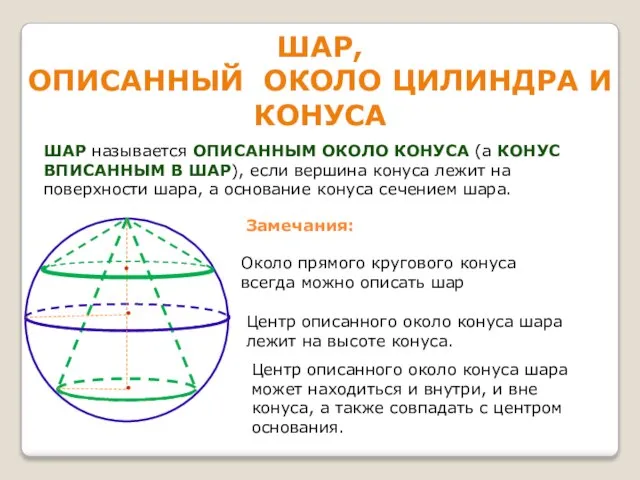 Шар, описанный около цилиндра и конуса
Шар, описанный около цилиндра и конуса Три диагностических признака простых форм средней категории. (Практическое занятие 6)
Три диагностических признака простых форм средней категории. (Практическое занятие 6) Этапы регресионно-корреляционного анализа с примером решения задачи
Этапы регресионно-корреляционного анализа с примером решения задачи Теорема Пифагора
Теорема Пифагора Площади геометрических фигур
Площади геометрических фигур Метод координат
Метод координат Высказывание. Операции над высказываниями
Высказывание. Операции над высказываниями С тех пор, как существует мирозданье, Такого нет, кто б не нуждался в знанье. Какой мы не возьмем язык и век - Всегда стремился к знанью человек…
С тех пор, как существует мирозданье, Такого нет, кто б не нуждался в знанье. Какой мы не возьмем язык и век - Всегда стремился к знанью человек… Презентация по математике "Устные упражнения на уроках геометрии. Аксиома измерения углов" - скачать
Презентация по математике "Устные упражнения на уроках геометрии. Аксиома измерения углов" - скачать  Презентация на тему Прямоугольный параллелепипед
Презентация на тему Прямоугольный параллелепипед  Элективный курс по математике. 11 класс. "Подводные рифы при подготовке к ЕГЭ"
Элективный курс по математике. 11 класс. "Подводные рифы при подготовке к ЕГЭ" Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Лекция №8 Двойные интегралы
Лекция №8 Двойные интегралы 8, 9 сандарына көбейту және бөлу кестесі
8, 9 сандарына көбейту және бөлу кестесі Примеры комбинаторных задач
Примеры комбинаторных задач Гектар
Гектар Распределительный закон умножения
Распределительный закон умножения Сравнение обыкновенных дробей
Сравнение обыкновенных дробей Теория множеств. Основные понятия теории множеств
Теория множеств. Основные понятия теории множеств Презентация на тему Арифметические действия с дробями
Презентация на тему Арифметические действия с дробями Вычисления в MATLAB
Вычисления в MATLAB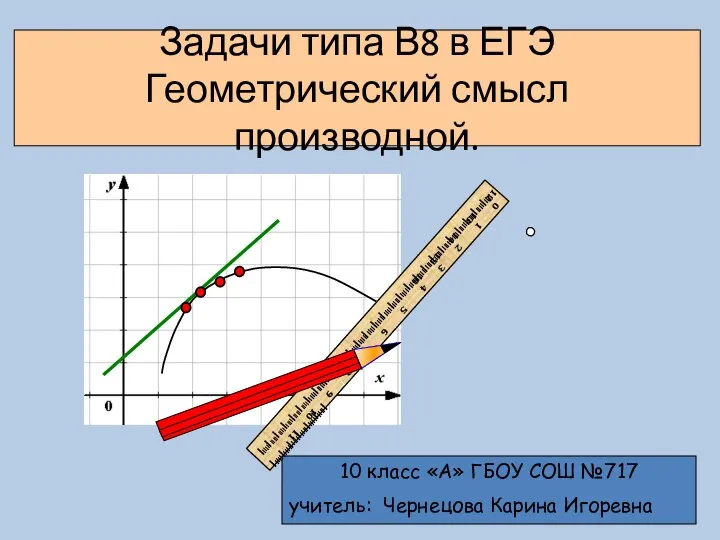 Геометрический смысл производной. Задачи типа В8 в ЕГЭ
Геометрический смысл производной. Задачи типа В8 в ЕГЭ